Fibonacci Numbers
Aug 15, 2014#tech #fibonacci numbers #dynamic programming #maths
Nature has always been a great inspiration for humans. We always try to find some patterns in nature and that led to the discovery of Fibonacci Numbers.
The fibonacci sequence:
Where the starting numbers of the sequence can either be 0 and 1 or 1 and 1 . By definition, the next term of the sequence is the sum of previous two. One can find these numbers in number of branches in trees, fruit sprouts of a pineapple, arrangement of leaves on a stem etc. These numbers have many applications in real world, for example in the field of Computer Science they are used in pseudorandom number generators, analysis of the Fibonacci heap data structure, polyphase merge sort etc.
Computing Fibonacci Numbers
Our task here will be to compute nth fibonacci number. From the definition:
A naive recursive implementation in Python:
Let's see what happens if fib(5) is called:
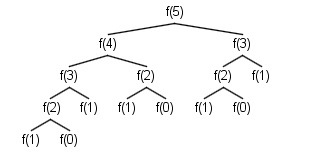
As you can observe fib(1) is called five times, which shows the redundancy in the algorithm.
Now let's analyse the time complexity of this algorithm.
At each level of recursion the condition check and addition takes constant time, O(1)
Therefore the recurrence relation of fib(n):
This recurrence relation turns out to be quite similar to the original fibonacci function. To get the lower bound, we can turn it into an inequality using the fact:
Now solving the recurrence relation:
To get to the base case T(0) = C(constant):
So, the running time of this naive algorithm is exponential! Well, how can we improve?
Dynamic Programming approach
As you have observed that there is redundancy in our recursive approach. To avoid redundancy we can store the computed value for further use (memoization). To achieve this I am going to use the Python dictionary, which provides constant time look-up from the keys.
This function computes the value of f(n - 1), f(n - 2), all the way down to f(1) and f(0) and then reuses it wherever required. The addition, comparison and dictionary look-up requires constant time, therefore the time complexity of this algorithm is:
So, fib_dp is a linear time algorithm. There's another way to implement it using bottom-up dynamic programming approach, which turns out to be quite similar to the next algorithm that I am going to discuss.
Intutive Iterative approach
In this approach we start with the first two numbers, add them to get next fibonacci number and update their values accordingly.
Here's the Python implementation:
The time complexity:
As you can see there's a tie in time complexity of fib_dp and fib_iter but fib_iter wins in space complexity as it requires constant amount of space.
Matrix Method
This one is the most complicated method of all the methods that we have discussed so far. It's based upon the following identity:
where F(n) is the nth fibonacci number. This formula can be easily proved by induction. So, the problem reduces to finding nth power of a matrix.
As a side note you can try to find the eigenvalues, eigenvectors and eigenbasis of the original matrix and then diagonalise it, to make it easier to find nth power of that matrix. You will end up with the following formula:
The problem with this formula is that it gives incorrect results with large values of n, as it involves the irrational number, square root of 5.
Let
The mathematical definition of (In our definition and not )
If we were to implement this function in Python, it will be a linear time algorithm. Now, let's make some minor changes in our definition:
The trick here is that we are going to compute only once and then squaring it (which is just multiplication by itself) to get the final result. For example 3^5 = 3 * 3 * 3 * 3 * 3 = 3^2 * 3^2 * 3. Note that we are assuming multiplication to be a constant time operation and that is why we prefer multiplication over recursive call of function. The time complexity of the Python implementation is going to be O(log n), since we are halving n on every level of recursion. This definition can also be applied to find nth power of numbers.
I will be using list of lists to represent a matrix in Python. Here is my implementation:
One thing that I would like to point out here is that as n becomes very large, our assumption that multiplication takes constant time will no longer be valid and it affects the overall time complexity.
Conclusion
Let's finish this off with comparing running time of our algorithms.
Here are the results for different values of n along with the time taken in seconds (these values may vary from machine to machine):
So, now you know how to effeciently compute nth fibonacci number!
I am open to suggestions, feel free to comment!
References:
http://en.wikipedia.org/wiki/Fibonacci_number
http://www.geeksforgeeks.org/program-for-nth-fibonacci-number/
0 1 1 2 3 5 8 13 21 34 55 89 144 233 ...
Where the starting numbers of the sequence can either be 0 and 1 or 1 and 1 . By definition, the next term of the sequence is the sum of previous two. One can find these numbers in number of branches in trees, fruit sprouts of a pineapple, arrangement of leaves on a stem etc. These numbers have many applications in real world, for example in the field of Computer Science they are used in pseudorandom number generators, analysis of the Fibonacci heap data structure, polyphase merge sort etc.
Computing Fibonacci Numbers
Our task here will be to compute nth fibonacci number. From the definition:
A naive recursive implementation in Python:
def fib(n):
if n <= 1: #base case
return n
return fib(n - 1) + fib(n - 2)
Let's see what happens if fib(5) is called:

As you can observe fib(1) is called five times, which shows the redundancy in the algorithm.
Now let's analyse the time complexity of this algorithm.
At each level of recursion the condition check and addition takes constant time, O(1)
Therefore the recurrence relation of fib(n):
This recurrence relation turns out to be quite similar to the original fibonacci function. To get the lower bound, we can turn it into an inequality using the fact:
Now solving the recurrence relation:
To get to the base case T(0) = C(constant):
So, the running time of this naive algorithm is exponential! Well, how can we improve?
Dynamic Programming approach
As you have observed that there is redundancy in our recursive approach. To avoid redundancy we can store the computed value for further use (memoization). To achieve this I am going to use the Python dictionary, which provides constant time look-up from the keys.
computed_fib = {} # cache
def fib_dp(n):
if n in computed_fib: # if already cached
return computed_fib[n]
if n <= 1:
fib = n
else:
fib = fib_dp(n - 1) + fib_dp(n - 2)
computed_fib[n] = fib # cache it
return fib
This function computes the value of f(n - 1), f(n - 2), all the way down to f(1) and f(0) and then reuses it wherever required. The addition, comparison and dictionary look-up requires constant time, therefore the time complexity of this algorithm is:
So, fib_dp is a linear time algorithm. There's another way to implement it using bottom-up dynamic programming approach, which turns out to be quite similar to the next algorithm that I am going to discuss.
Intutive Iterative approach
In this approach we start with the first two numbers, add them to get next fibonacci number and update their values accordingly.
Here's the Python implementation:
def fib_iter(n):
a, b = 0, 1
for i in range(n):
a, b = b, a + b # Python \m/
return a
The time complexity:
As you can see there's a tie in time complexity of fib_dp and fib_iter but fib_iter wins in space complexity as it requires constant amount of space.
Matrix Method
This one is the most complicated method of all the methods that we have discussed so far. It's based upon the following identity:
where F(n) is the nth fibonacci number. This formula can be easily proved by induction. So, the problem reduces to finding nth power of a matrix.
As a side note you can try to find the eigenvalues, eigenvectors and eigenbasis of the original matrix and then diagonalise it, to make it easier to find nth power of that matrix. You will end up with the following formula:
(
Binet's formula)
The problem with this formula is that it gives incorrect results with large values of n, as it involves the irrational number, square root of 5.
Let
The mathematical definition of (In our definition and not )
If we were to implement this function in Python, it will be a linear time algorithm. Now, let's make some minor changes in our definition:
The trick here is that we are going to compute only once and then squaring it (which is just multiplication by itself) to get the final result. For example 3^5 = 3 * 3 * 3 * 3 * 3 = 3^2 * 3^2 * 3. Note that we are assuming multiplication to be a constant time operation and that is why we prefer multiplication over recursive call of function. The time complexity of the Python implementation is going to be O(log n), since we are halving n on every level of recursion. This definition can also be applied to find nth power of numbers.
I will be using list of lists to represent a matrix in Python. Here is my implementation:
X = [[1, 1], [1, 0]]
def matrix_mul(A, B): # Multiplies two 2x2 matrices
return [[A[i][0] * B[0][j] + A[i][1] * B[1][j] for j in range(2)]\
for i in range(2)]
def pow_matrix(A, n):
if n <= 1:
return A
B = pow_matrix(A, n / 2) # A ^ floor(n / 2)
C = matrix_mul(B, B) # B ^ 2
if n % 2:
return matrix_mul(A, C)
return C
def fib_matrix(n):
if n == 0:
return 0
return pow_matrix(X, n - 1)[0][0] # Why n - 1 ?
One thing that I would like to point out here is that as n becomes very large, our assumption that multiplication takes constant time will no longer be valid and it affects the overall time complexity.
Conclusion
Let's finish this off with comparing running time of our algorithms.
import time t = time.time() print fib(n) print time.time() - t t = time.time() print fib_dp(n) print time.time() - t t = time.time() print fib_iter(n) print time.time() - t t = time.time() print fib_matrix(n) print time.time() - t
Here are the results for different values of n along with the time taken in seconds (these values may vary from machine to machine):
| n | fib | fib_dp | fib_iter | fib_matrix |
| 10 | 0.0090000629425 | 0.00599980354309 | 0.00600004196167 | 0.00600004196167 |
| 40 | 99.8289999962 | 0.00899982452393 | 0.0090000629425 | 0.00999999046326 |
| 100 | X | 0.0199999809265 | 0.010999917984 | 0.010999917984 |
| 1000 | X | X | 0.018000125885 | 0.0169999599457 |
| 100000 | X | X | 1.46300005913 | 1.02699995041 |
| 1000000 | X | X | 88.7419998646 | 43.2999999523 |
So, now you know how to effeciently compute nth fibonacci number!
I am open to suggestions, feel free to comment!
References:
http://en.wikipedia.org/wiki/Fibonacci_number
http://www.geeksforgeeks.org/program-for-nth-fibonacci-number/